

What does a hexagon tessellate with?ģ60 divided by 90 = 4 this is why squares are able to tessellate. Since 108 does not divide 360 evenly, the regular pentagon does not tessellate this way. In order for a regular polygon to tessellate vertex-to-vertex, the interior angle of your polygon must divide 360 degrees evenly. There are only three shapes that can form such regular tessellations: the equilateral triangle, square, and regular hexagon.Ī regular pentagon does not tessellate. Therefore, there are only three regular tessellations.

Can a 12 sided shape tessellate?Įquilateral triangles, squares and regular hexagons are the only regular polygons that will tessellate.
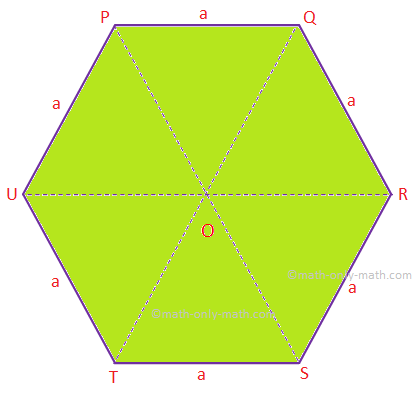
#CREATE REGULAR HEXAGON GSP5 SERIES#
Not only do they not have angles, but you can clearly see that it is impossible to put a series of circles next to each other without a gap. Tessellations can be used for tile patterns or in patchwork quilts!Ĭircles or ovals, for example, cannot tessellate. You can even tessellate pentagons, but they won’t be regular ones. You can have other tessellations of regular shapes if you use more than one type of shape. Triangles, squares and hexagons are the only regular shapes which tessellate by themselves. But, if we add in another shape, a rhombus, for example, then the two shapes together will tessellate.Ī regular pentagonal tiling on the Euclidean plane is impossible because the internal angle of a regular pentagon, 108°, is not a divisor of 360°, the angle measure of a whole turn. A regular pentagon does not tessellate by itself. Using these extensions, this simple and straightforward method can be used to construct polygons of any \(n\) to any precision desired using only the classic geometric instruments.Therefore, every quadrilateral and hexagon will tessellate.
The rule may be extended in simple manners-either by better approximating \(\pi\), or by superconstruction/division. We have presented a successful general rule for the approximate construction of regular polygons.
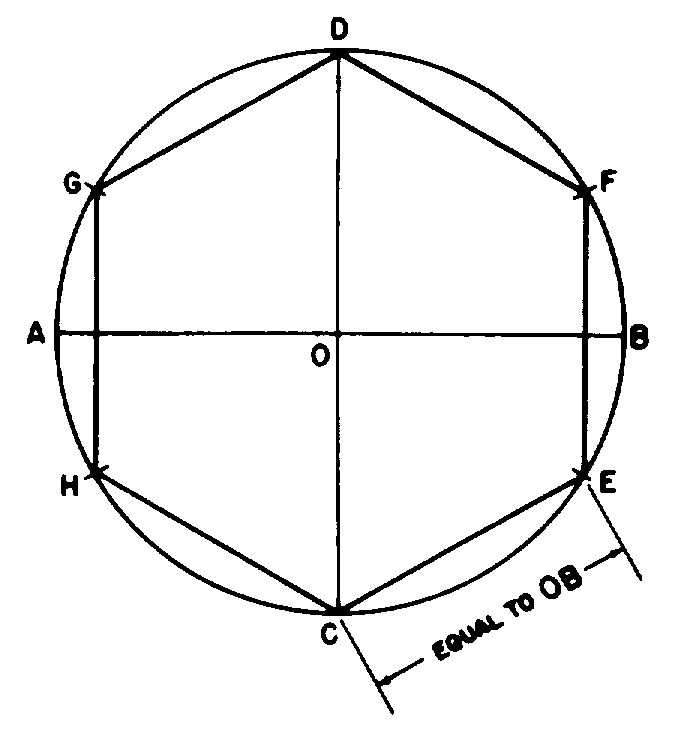
It is worth noting that regular polygons of any degree may be constructed to arbitrary precision using this method. We call this process "superconstruction/division". However, Russ suggests that, for a highly accurate polygon of small \(n\), one could merely construct a polygon with a convenient integer multiple of \(n\) sides, but only connect a corresponding fraction of the vertices (for example, construct a regular \(21\)-gon, and connect every third vertex to form a heptagon. Values \(n < 4\) are not included both formulas are terrible for triangles, and exact constructions exist for \(n < 7\) anyway.Īfter using common exact constructions for \(n = 3, 4, 5,\) and \(6\), one might reasonably continue with the Equation 1 approximation for \(n = 7, 9, 11, 13,\) and \(14\), with Equation 2 for higher \(n\) where inexact constructions are impossible. Then, using a compass set to \(c := \frac\).įigure 3: Accuracy of fraction of the radius procedure. To replicate Ian's initial efforts, using standard geometric techniques, one may draw a circle of radius \(a\), then divide the radius of the circle into \(15\) segments of equal length. We term this algorithm, and its improvements, the "fraction of a radius" technique.ĭiscussion: Figure 1: Approximate construction of a regular heptagon via the "fraction of the radius" technique. With assistance, the algorithm was generalized to construct polygons for any \(n\). The algorithm was then extended for the construction of a nonagon (comparing favorably with traditional constructions, as shown by Dixon: ). The geometry computer program "Geometer's Sketchpad" was used to develop a construction for an approximate regular heptagon (for comparison, other procedures for doing this have been described by Dixon: Mathographics. Ian, then 14, was interested in finding approximate and practical ways to construct regular polygons that are impossible to construct exactly if using only a compass and straightedge. We develop a practical general procedure for the approximate construction of regular polygons which works well for large \(n\) and which can be adapted for small \(n\). Some regular polygons with \(n\) sides are classically "constructible" using only a compass and a straightedge, whereas others have been proven by Gauss to be "unconstructable", at least exactly. Ian Mallett, Brenda Mallett, Russell Mallett, Updated Ian Mallett, Approximate Construction of Regular Polygons


 0 kommentar(er)
0 kommentar(er)
